
前言
算法是程序员的核心科技。算法的作用毋庸置疑,在计算机科学中随处可见担任着核心的作用,如地图导航、数据检索、图形渲染、游戏、机器人等等,最近的神经网络、人工智能、大数据等等概念中,算法的重要性不言而预。
正如现在大量的人从传统行业转入计算机行业,以后计算机行业也会逐渐没落,转而进入人工智能的时代,其实人类一直以来都在扩充着自己的边界,直接的体现就是受教育时间的增长。
基础概念
首先得理解一些基础的概念:
- 算法是数学的一种,我们可以使用任何一种语言来描述它,包括口语。
- 在计算机中,算法和数据结构是结合的。算法需要考虑数据在计算机中的存储位置。
- 我们使用时间复杂度和空间复杂度来度量算法消耗计算机资源的大小,分别代表了算法所用计算时间和存储大小,且在多数情况下,实现同一功能的不同算法在时间复杂度和空间复杂度有自己的优势,也就是说时间复杂度和空间复杂度可以互相转换。
算法即是数学,但算法有自己的一套数学基础,用做性能分析:
引入了4个基本的数学定义,这些定义的主要目的是在函数间建立一种相对的级别:
例如:当我们描述一个算法 1000N = O(N^2) 是什么意思?
设:算法本身的函数为 T(N)
- O( f(N) ),读作“大O”,代表:T(N)的增长率 <= f(N),则记为 T(N) = O( f(N) ); 用于度量上限。(此处当 n < 1000 时,T(N)的增长率要> f(N),当此类函数,总存在一个常数,以至于等式成立,由此忽略常数)
- Ω( f(N) ),读作“omega”,代表:T(N) 的增长率 >= f(N),用于度量下限。
- θ( f(N) ),读作“theta”,代表:T(N) 的增长率 = f(N)。
- ο( f(N),读作“小o”,代表:T(N) 的增长率 < f(N)。
得: 忽略常数的影响,1000N 的增长速度小于 N^2,所以 1000N 可以用 O(N^2) 来描述
例:
N^3 = Ω( N^2)
2N^2 = θ( N^2)
另外,对于 2N^2 来说,用 O(N^4)、O(N^3)、O(N^2)、θ( N^2) 来描述从定义上来说都是可以的,但着其中有最好的答案,根据具体上下文最好的答案可能会有不同。
推倒定理
根据定义可以得到:
法则一:
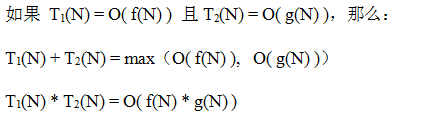
法则二:
如果 T(N) 是一个 k 次多项式,则 T(N) = θ(N^k)。
法则三:
我们总能通过计算极限 lim f(N)/g(N) 来确定两个函数 f(N) 和 g(N) 的相对增长率,必要的时候可以使用诺必达法则。
极限是 0,则 f(N) = o( g(N) ),
极限是 c ≠ 0,则 f(N) = θ( g(N) ),
极限是 ,则 g(N) = o( f(N) ),
极限摆动,二者无关。
参考
马克·艾伦·维斯. 数据结构与算法分析:C语言描述(原书第二版). 机械工业出版社